Congruence of Triangles By AAS Criteria
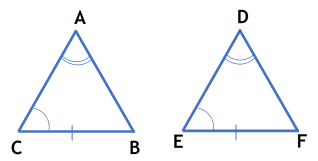
Congruence of Triangles by AAS Criteria
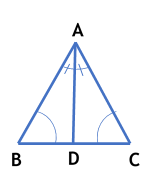
Theorem : If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
|
Given: Two To Prove: Proof: We have, Similarly,
Arrange the terms, we have
Thus, in Now, in BC = EF [Given] and, So, by ASA criterion of congruence, Hence Proved |
 |
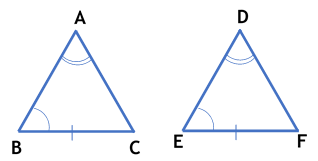Theorem: If two angles of a triangle are equal. then sides opposite to them are also equal.
|
Given: A To Prove: AB = AC Construction: Draw the bisector of Proof: In So, by AAS criterion of congruence, we have
|
 |
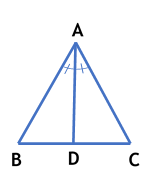Illustration: If is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
Solution: In , we have
AB = AC [Given]
..........................(i) [
Angles opposite to equal sides are equal]
Now, in , we have
[From (i)]
[Each equal to
]
and, BD = BC [Common]
So, by AAS criterion of congruence, we have
[
Corresponding parts of congruent triangles are equal]
Hence, BD = CE
If the two triangles are congruent by AAS criteria. | |||
| Right Option : B | |||
| View Explanation | |||
In figure given below, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Then | |||
| Right Option : D | |||
| View Explanation |
In the figure given below, AD is a median and BL,CM are perpendiculars drawn from B and C respectively on AD and AD produced. Then BL = CM by CPCT using which criteria on congruence? | |||
| Right Option : D | |||
| View Explanation | |||
Students / Parents Reviews [10]
It was a good experience with Abhyas Academy. I even faced problems in starting but slowly and steadily overcomed. Especially reasoning classes helped me a lot.
Cheshta
10thMy experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.
Shivam Rana
7thAbhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.
Manish Kumar
10thMy experience was very good with Abhyas academy. I am studying here from 6th class and I am satisfied by its results in my life. I improved a lot here ahead of school syllabus.
Ayan Ghosh
8thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.
Archit Segal
7thIt has a great methodology. Students here can get analysis to their test quickly.We can learn easily through PPTs and the testing methods are good. We know that where we have to practice
Barkha Arora
10thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying
Yatharthi Sharma
10thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.
Shreya Shrivastava
8thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.
Hiya Gupta
8thBeing a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from my daughter.
