Available Online Courses for selected Class / Category
NTSE
10th NTSE
BASIC
Free
Self Learning
Free Topics
(Click here to know About SELF LEARNING)
MOCK TESTS
Few Available
(Click here to attempt Free Mock Test)
Concepts Learning Progress
Available
Course Progess
Self Learning Progress
Report Card
Revision / Exam Preparation
Theory Notes
Question Bank
Subjects Related Concepts
Test Generator
Free Topics
Reports
Available as Required.
VIDEOS
Few Available
NTSE
10th NTSE
Self Learning
₹17200 ₹12000 +
Taxes
Self Learning
Available
(Click here to know About SELF LEARNING)
MOCK TESTS
65
(Click here to attempt Free Mock Test)
Concepts Learning Progress
Available
Test Generator
Syllabus / Topic Test
Solution and Detailed Analysis
Course Progess
Self Learning Progress
Report Card
Revision / Exam Preparation
Theory Notes
Test Generator
Subjects Related Concepts
Self Learning
Videos
Self Learning Exams
Practice
Self Learning - At Own Pace
Question Answers with Explaination
Reports
Question-wise Analysis
Strong, Moderate and weak Concepts
Remedial Tests for Weak Concepts
Achievements - Month/Subject & Subject / Month
Self Study Detail
Graphical View
Your Rankings - Month / Subject & Subject / Month
VIDEOS
799
SUBJECTS
Maths, Physics, Chemistry, Biology, English, History, Democratic Politics, Geography, Economics, Verbal Reasoning, Non Verbal Reasoning, Vedic Maths

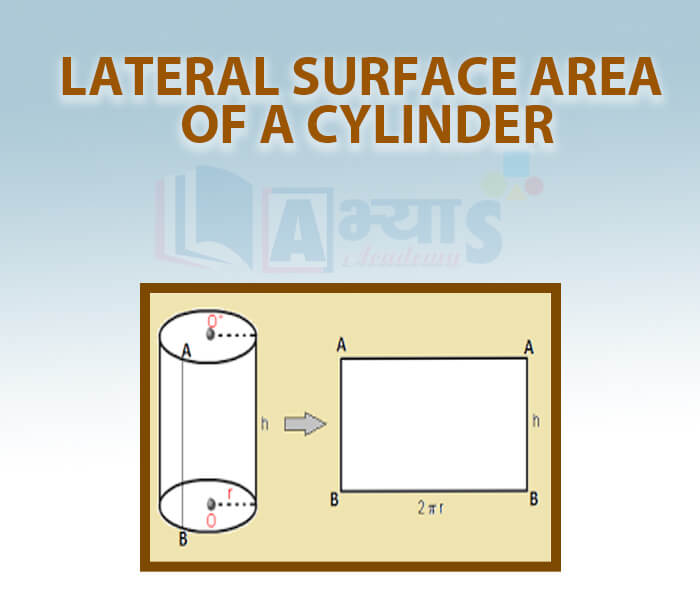
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)



