Resistance Depends on Area of Cross Section





Resistance Depends on Area of Cross Section
Resistance Depends on the Area of Cross Section of the wire:
The resistance of ohmic circuit elements such as metal wires or carbon resistor depends on the area of cross section of the wire. If we fix the length of the copper wire and vary the thickness or cross-sectional area A then we find the resistance of the copper decreases as the cross-sectional area A of the wire increases. To find dependence,we will follow the following steps
1 Keep the length of the wire as fixed and just increase or decrease the area of cross section of the wire.
2. Apply a potential difference across the ends of the wire and calculate the value of R from the values of current and potential difference
3. Calculate the value of R for different values of the area of cross section of the wire.
4. Plot a graph as shown below by taking the reciprocal of area of cross section along x axis and resistance along y axis

From the first graph we observe that as the reciprocal of area of cross section increases the resistance also increases. So we find that there is a proportionality between the reciprocal of area of cross section A of the wire and the resistance of the wire R. The resistance of a conductor R is directly proportional to the reciprocal of area of cross section
5. We can also plot a graph as shown below by taking the area of cross section along x axis and resistance along y axis
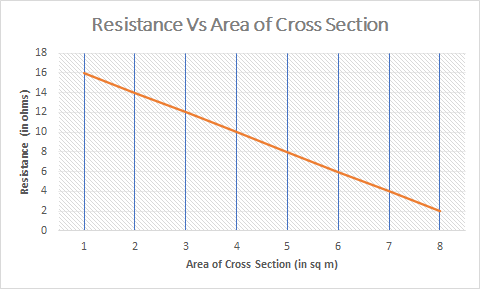
From this graph we observe that as the area of cross section increases the resistance decreases. So we find that there is a proportionality between the area of cross section A of the wire and the resistance of the wire R. The resistance of a conductor R is inversly proportional to the area of cross section
In fact we get an inverse relationship between area of cross section and resistance and it can be stated as
We know that Resistance is directly proportional to the length of the wire. It can be stated that
Combining the expressions of relation of resistance with length and area of cross section of a wire we get
:
To simplify this expression, we can replace the product of the two constants with a single new constant and write
This constant is known as as Resistivity and it depends on the material of the conductor.
Illustration: In a circuit when a current of 2 A flows through a certain wire having resistance R a potential difference of 8 V is generated across the wire. What will be the new potential difference generated across the wire if the area of cross section of the wire is doubled.
Solution: It is given that
V= 8 V
I = 2 A
R= ?
V= IR
As the area of cross section of the wire is doubled so the resistance will be halved because resistance is inversely proportional to area of cross section..
So new potential difference of 4V is generated across the wire if the area of cross section of the wire is doubled.
Illustration: Calculate the resistance of a conductor when its length is doubled
Solution: We are given that the length is doubled so
Original Length = l1
New Length = l2
We know that
Let Original Resistance be R1 and New Resistance be R2. So
Substituting the value of New length we get
Hence when length of a conductor is doubled its resistance gets doubled.
Illustration: A certain wire has a resistance R. Find the resistance of another wire made of same material but its area of cross-section is doubled.
Solution: We are given that the area of cross section is doubled so
Original Area of Cross Section = A1
New Area of Cross Section = A2
We know that
Let Original Resistance be R1 and New Resistance be R2. So
Substituting the value of New length we get
Hence we can say that as area of cross-section is doubled the resistance is halved
If the length of a wire is 3 km and its diameter is 2 cm, then calculate its resistance.
| |||
| Right Option : B | |||
| View Explanation | |||
Resistivity of a conductor depends on ______________________. | |||
| Right Option : D | |||
| View Explanation | |||
Resistance of some materials decreases with increase of temperature. These materials are ____________________ . | |||
| Right Option : D | |||
| View Explanation | |||
Students / Parents Reviews [10]
My experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.

Shivam Rana
7thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying

Yatharthi Sharma
10thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.

Archit Segal
7thAbhyas is a complete education Institute. Here extreme care is taken by teacher with the help of regular exam. Extra classes also conducted by the institute, if the student is weak.

Om Umang
10thIt was a good experience with Abhyas Academy. I even faced problems in starting but slowly and steadily overcomed. Especially reasoning classes helped me a lot.

Cheshta
10thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.

Hiya Gupta
8thMy experience was very good with Abhyas academy. I am studying here from 6th class and I am satisfied by its results in my life. I improved a lot here ahead of school syllabus.

Ayan Ghosh
8thAbhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.

Manish Kumar
10thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.

Eshan Arora
8thIt has a great methodology. Students here can get analysis to their test quickly.We can learn easily through PPTs and the testing methods are good. We know that where we have to practice
