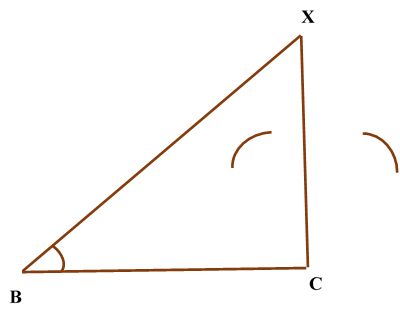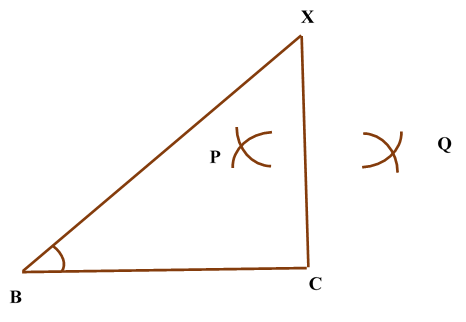| e-NOTES (1038 [C] ) | ||||||||||||||||||||||||||
| 9th (Maths) | |||||||||||||||||||||||||||
| Constructions | |||||||||||||||||||||||||||
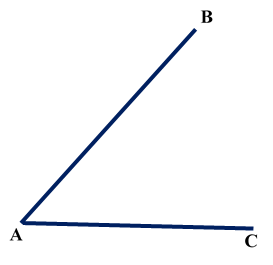
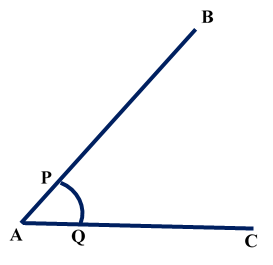
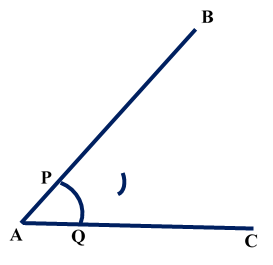
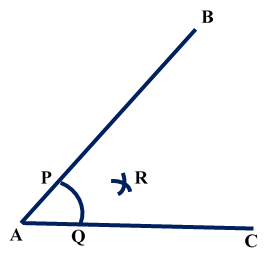
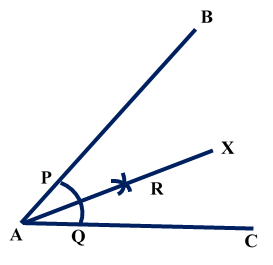
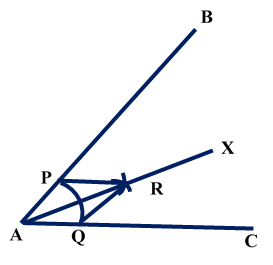
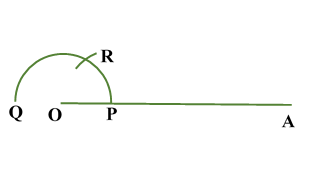
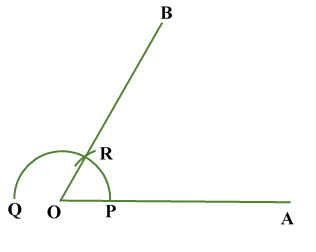
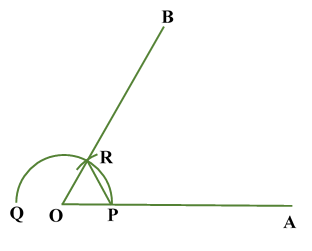
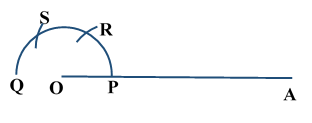
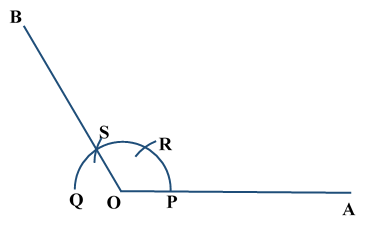
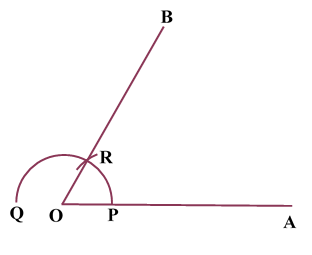
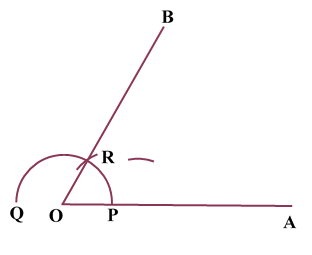
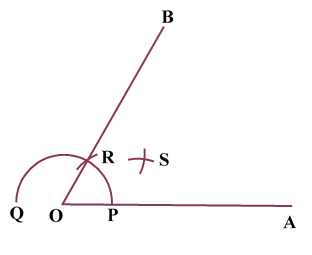
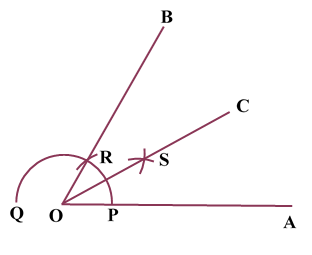
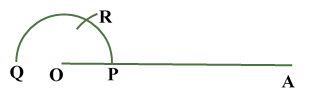
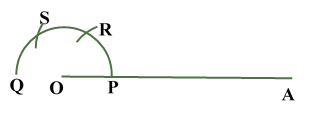
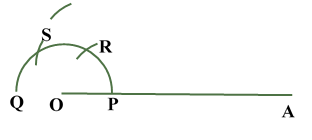
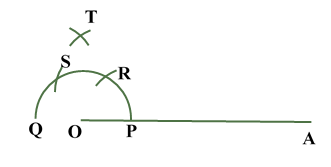
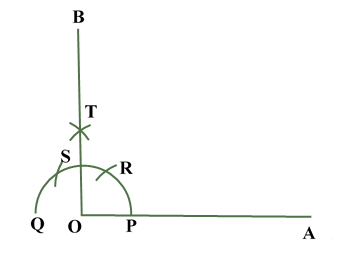
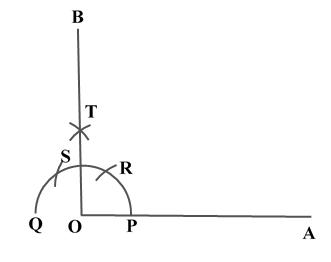
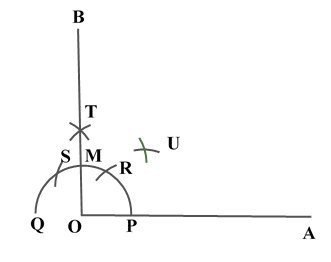
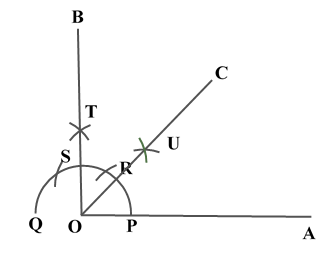
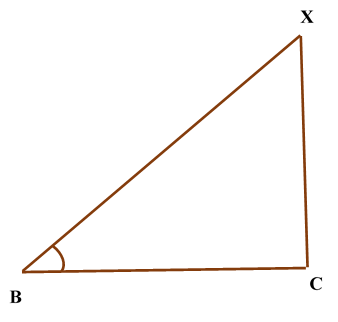
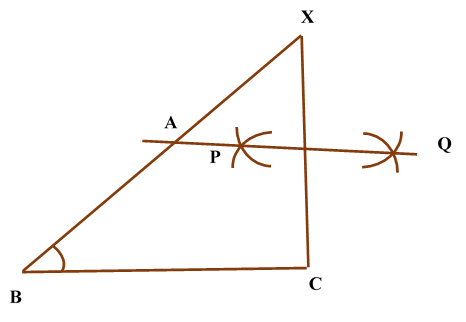
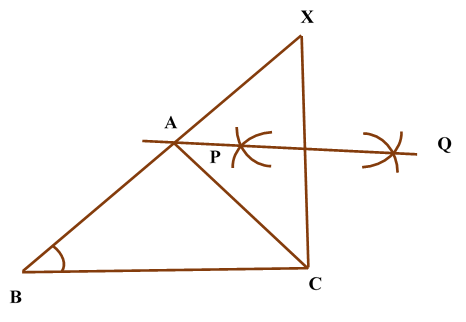
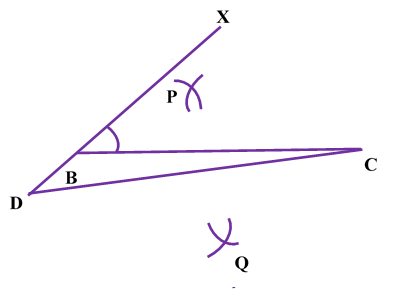
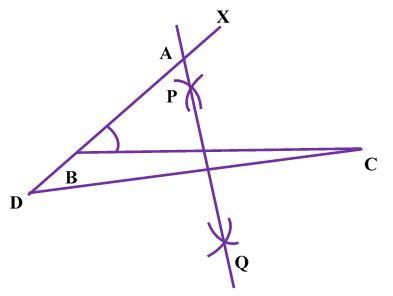
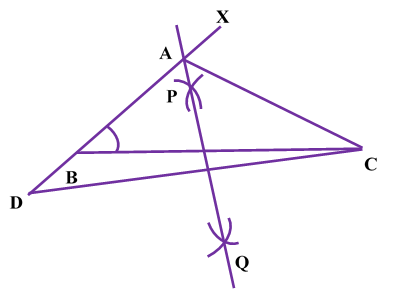
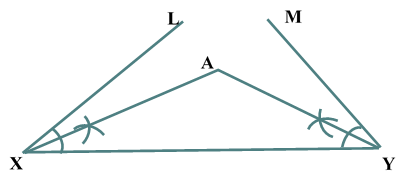
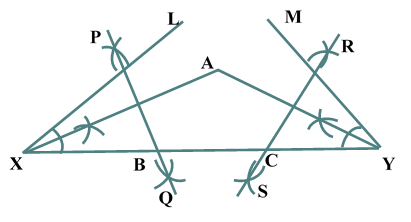
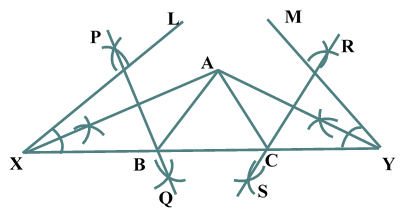
Construction of Angle and Angle BisectorBisecting an angle means drawing a ray in the interior of the angle, with its initial point at the vertex of the angle such that it divides the angle into two equal parts .
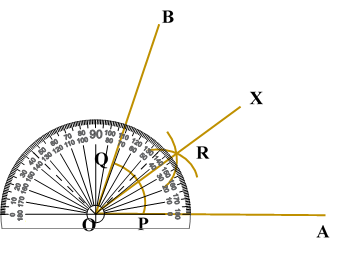
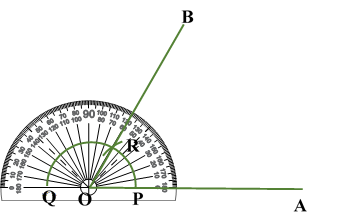
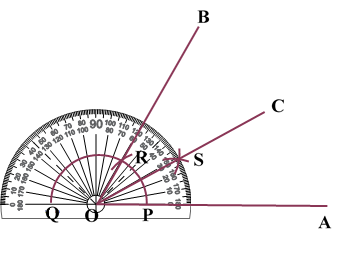
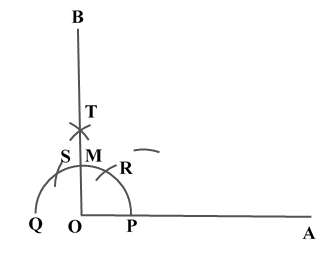
Verification: Measure Justification: Now let us see how this method gives us the required angle bisector.
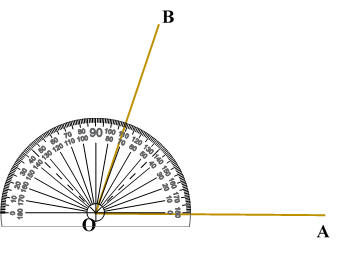
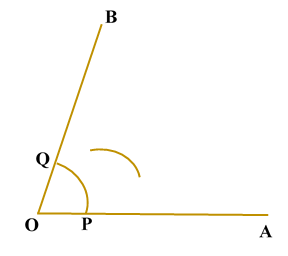
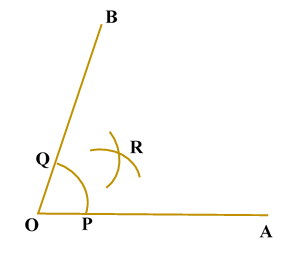
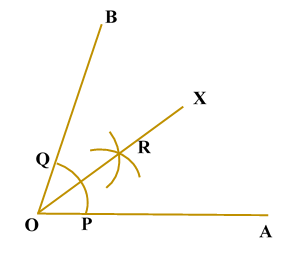
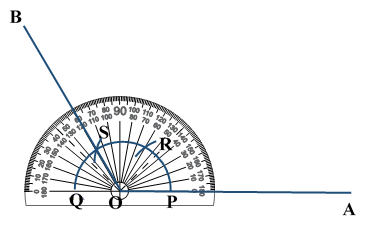
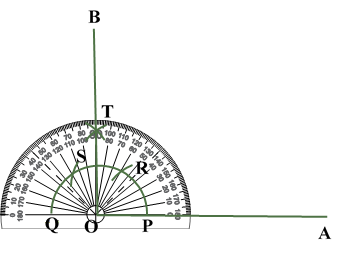
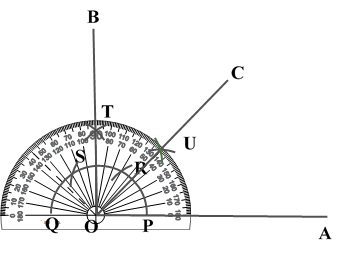
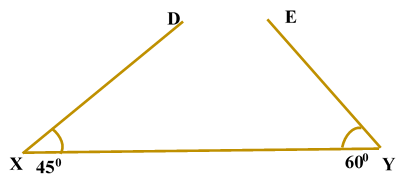
ILLUSTRATION: Using a protractor, draw an angle of mesure SOLUTION We follow the following steps to draw an angle of Steps of Construction
| |||||||||||||||||||||||||||
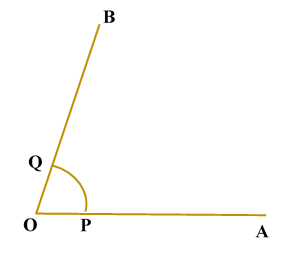
Construction of 60 Degree AngleCONSTRUCTION OF 60 DEGREE ANGLE: In order to construct an angle of Steps of Construction
Justification : Now, let us see how this method gives us the required angle of
CONSTRUCTION OF AN ANGLE OF In order to construct an angle of Steps of Construction
| |||||||||||||||||||||||||||
Construction of 30 Degree AngleConstruction of 30 Degree Angle : In order to contruct an angle of Steps of Construction
| |||||||||||||||||||||||||||
Construction of 90 Degree AngleConstruction of 90 Degree Angle: In order to construct an angle of measure of Steps of Construction
Construction of an angle of Steps of Construction
| |||||||||||||||||||||||||||
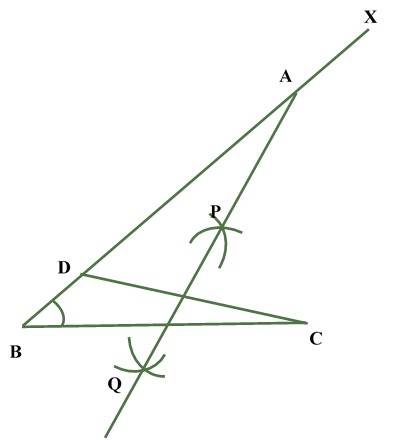
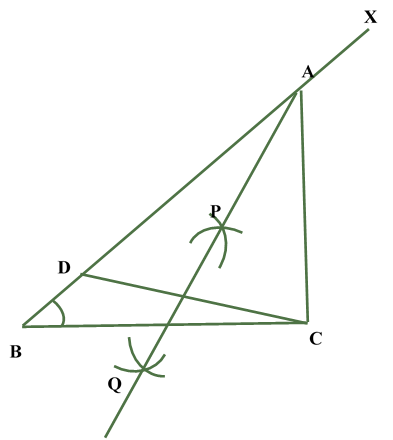
Construction of a triangle given its base and base angle and sum of other two sidesIn order to construct a triangle, when its base, sum of the other two sides and one of the base angles are given, we follow the following steps: Steps of Construction: Obtain the base, base angle and the sum of other two sides. Let BC be the base,
Justification: Let us now see how do we get the required triangle. Since point A lies on the perpendicular bisector of CX.Therefore, AX = AC Now, BA = BX - AX
PROOFSTEP I Obtain the base, base angle and the sum of other two sides. Let AB be the base, STEP II Draw the base AB. STEP III Draw STEP IV From ray AX, cut-off line segment AD equal to l ( the sum of other two sides). STEP V Join BD. STEP VI Construct an angle STEP VII Suppose BY intersects AX at C. Then, Justification: Let us now see how do we get the required triangle. In
Now, AC = AD - CD
Example : Construct a triangle ABC in which AB = 5.8 cm , BC + CA = 8.4 cm and SOLUTION In order to construct the Steps of Construction STEP I Draw AB = 5.8 cm STEP II Draw STEP III From ray BX, cut off line segment BD = BC + CA = 8.4 cm. STEP IV Join AD STEP V Draw the perpendicular bisector of AD meeting BD at C. STEP VI Join AC to obtain the required triangle ABC. Justification: Clearly, C lies on the perpendicular bisector of AD.
Now, BD = 8.4 cm
Hence, | |||||||||||||||||||||||||||
Construction of a triangle given a base and base angle and the difference of other two sidesConstruction of a triangle given a base and base angle and the difference of other two sides : In order to contruct a triangle when its base, difference of the other two sides and one of the base angles are given, we follow the following steps: Steps of Contruction: Obtain the base, base angle and the difference of two other sides. Let BC be the base, Case I: AB > AC i.e., x =AB - AC
Case II: AC > AB i.e., x =AC - AB
Justification: Let us now see how do we get the required triangle. Since A lies on the perpendicular bisector of DC.
So, BD = AD - AB = AC - AB Example : Construct a triangle ABC in which base AB = 5 cm, SOLUTION In order to construct the triangle ABC, we follow the following steps: Steps of Construction: STEP I Draw base AB = 5 cm STEP II Draw STEP III From ray AX, cut off line segment AD = 2.5 cm(=AC-BC) STEP IV Join BD. STEP V Draw the perpendicular bisector of BD which cuts AX at C. STEP VI Join BC to obtain the required triangle ABC. Justification: Since C lies on the perpendicular bisector of DB. THerefore, CD = CB Now, AD = 2.5 cm
Hence, | |||||||||||||||||||||||||||
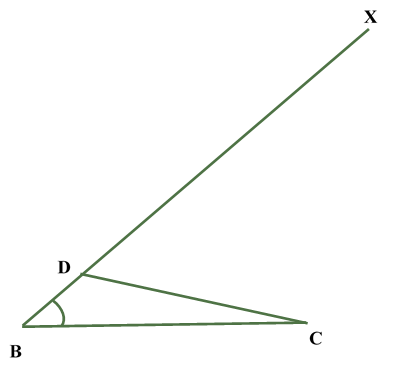
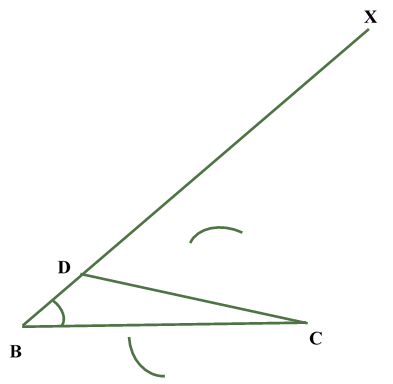
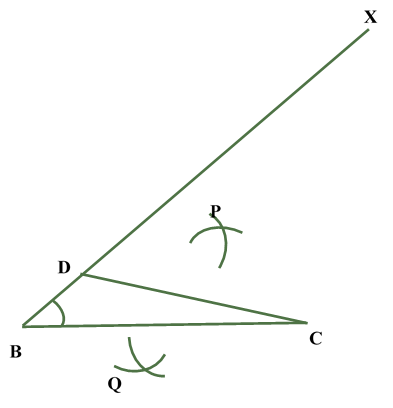
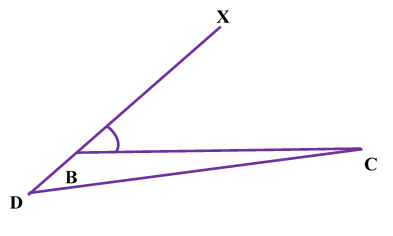
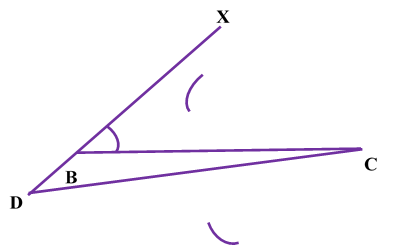
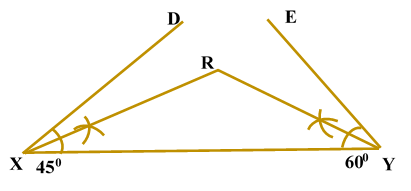
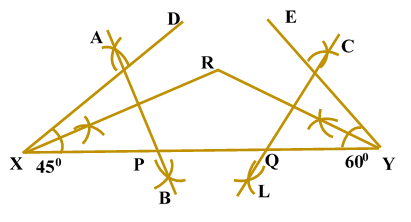
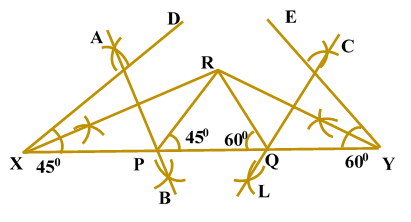
Construction of a triangle given its perimeter and its two base anglesConstruction of Triangle Given Its Perimeter and Its Two Base Angles: In order to construct a triangle of given perimeter and two base angles, we follow the following steps: Steps of Construction: Obtain the perimeter and the base angles of the triangle.Let ABC be a triangle of perimeter p cm and base BC.
Justification: For the justification of the construction, we observe that B lies on the perpendicular bisector of AX.
Similarly, C lies on the perpendicular bisector of AY.
Now, XY = XB + BC + CY
In = In Example: Construct a triangle PQR whose perimeter is equal to 14 cm, SOLUTION To draw Steps of Construction:
| |||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||

Powered by ABHYAS ChatBOT.

What describes you best?

I am a Student
I am a Tutor
I am a School Owner
I want to appear for Govt. Exams