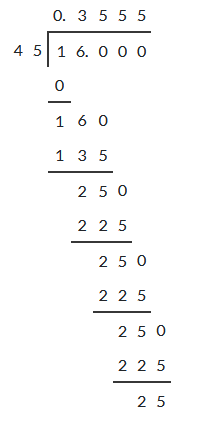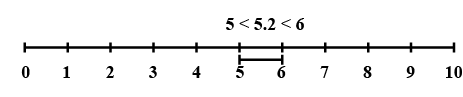ABHYAS | Self Learning | Testing Platform | ABHYAS

ERR - 9th - Maths [Number System II]

		e-NOTES (1060 [C] )
9th (Maths)
Number System II
Converting Non Terminating Repeating Decimals into Fractions Non Terminating Repeating Decimals: The rational numbers which when expressed in decimal form by division method, no matter how long they are divided, they always leave a remainder . In other words, the division process never comes to an end. This is due to the reason that in the division process the remainder starts repeating after a certain number of steps. In such cases, a digit or a block of digits repeats itself.For example, 0.3333...,0.1666666....,0.123123123....,1.2692307692307692307.... etc. Such decimals are called non-terminating repeating or recurring decimals. These decimal numbers are represented by putting a bar over the first block of the repeating part and omit the other repeating blocks. Thus, we write $0.33333 ...= 0.bar{3}$ , $0.16666... =0.1overline{6}$ $0.123123123 .. =0.overline{123}$ and $1.26923076923076292307 ... =1.2overline{692307}$ . Illustration: Find the decimal representation of $frac{-16}{45}$ Solution: By long division, we have $therefore ;;frac{16}{45}=0.3555...=0.3overline{5}$ Hence, $large frac{-16}{45}=-0.overline{35}$ Converting Non Terminating Repeating Decimals into Fractions: In a non-terminating repeating decimal, there are two types of decimal representation. (i) A decimal in which all the digits after the decimal point are repeated. These types of decimals are known as pure recurring decimals. For example: $large 0.bar{6},0.overline{16},0.overline{123}$ are pure recurring decimals. (ii) A decimal in which at least one of the digits after the decimal point is not repeated and then some digit or digits are repeated.This type of decimals are known as mixed recurring decimals. For example $large 2.1overline{6},0.3overline{5},0.7overline{85}$ are mixed recurring decimals. Conversion of a Pure Recurring Decimal to the Form: In order to convert a pure recurring decimal to the form $frac{p}{q}$ , we follow the following steps: Step 1 Obtain the repeating decimal and put it equal to x (say). Step 2: Write the number in decimal form by removing bar from the top of repeating digits and listing repeating digits at least twice. For example, write $x=0.bar{8}$ as $x=0.888$ ......and $x=0.overline{14}$ as $x=0.141414....$ Step 3: Determine the number of digits having bar on their heads. Step 4: If the repeating decimal has 1 place repetition, multiply by 10 for a two place repetition, multiply by 100 and for a three place repetition, multiply by 1000 and so on. Step 5: Subtract the number in step 2I from the number obtained in step 4 Step 6: Divide both sides of the equation by the coefficient of x. Step 7: Write the rational number in its simplest form. The following examples will illustrate the above procedure. Illustration : Express of the following decimals in the form $frac{p}{q}$ $large (i);0.bar{1}$ $large (ii);0.bar{2}$ $large (iii);0.bar{3}$ $large (iv);0.bar{4}$ $large (v);0.bar{5}$ $large (vi);0.bar{6}$ Solution: (i) Let $x=0.bar{1}$ . Then, x = 0.11111... ........[1] As only one digit is repeating multiply both sides with 10 $large Rightarrow$ 10x = 1.11111... .......[2] On subtracting (1) from (2) , we get 9x = 1 $Rightarrow ;;;x=frac{1}{9}$ $Rightarrow ;;;0.bar{1}=frac{1}{9};;i.e.,0.11111....=frac{1}{9}$ (ii) Let $large x=0.bar{2}.$ Then, x = 0.222222..... $large Rightarrow$ 10x =2.222222.... On subtracting (i) from (ii), we get 9x = 2 $large Rightarrow ;;x=frac{2}{9}$ $large Rightarrow ;;0.bar{2}=frac{2}{9};;i.e., 0.22222....=frac{2}{9}$ (iii) Let $large x=0.bar{3}.$ Then, x = 0.33333...... $large Rightarrow$ 10x = 3.33333..... On subtracting (i) from (ii) , we get 9x = 3 $large Rightarrow ;;x=frac{3}{9}$ $large Rightarrow ;;0.bar{3}=frac{3}{9};i.e.,0.33333...=frac{3}{9}$ Proceeeding as above, we obtain $large 0.bar{4}=frac{4}{9};i.e.,0.44444...=frac{4}{9}$ $large 0.bar{5}=frac{5}{9};i.e.,0.55555...=frac{5}{9}$ $large 0.bar{6}=frac{6}{9};i.e.,0.66666...=frac{6}{9}$ Also, we have $large 0.bar{7}=frac{7}{9};i.e.,0.77777...=frac{7}{9}$ $large 0.bar{8}=frac{8}{9};i.e.,0.88888...=frac{8}{9}$ and, $large 0.bar{9}=frac{9}{9};i.e.,0.99999...=frac{9}{9}$ REMARK It follows from the above example that $large 0.bar{1}=frac{1}{9},0.bar{2}=frac{2}{9}=2timesfrac{1}{9}=2times0.bar{1}$ $large 0.bar{3}=frac{3}{9}=3timesfrac{1}{9}=3times0.bar{1}$ $large 0.bar{4}=frac{4}{9}=4timesfrac{1}{9}=4times0.bar{1}$ $large 0.bar{5}=frac{5}{9}=5timesfrac{1}{9}=5times0.bar{1}$ $large 0.bar{6}=frac{6}{9}=6timesfrac{1}{9}=6times0.bar{1}$ $large 0.bar{7}=frac{7}{9}=7timesfrac{1}{9}=7times0.bar{1}$ $large 0.bar{8}=frac{8}{9}=8timesfrac{1}{9}=8times0.bar{1}$ $large 0.bar{9}=frac{9}{9}=9timesfrac{1}{9}=9times0.bar{1}$ Conversion of a Mixed Recurring Decimal to the Form $large frac{p}{q}$ While converting a recurring decimal that has one or more digits before the repeating digits, it is necessary to isolate the repeating digits. In order to convert a mixed recurring decimal to the form $large frac{p}{q}$ , we follow the following steps: Step 1: Obtain the mixed recurring decimal and write it equal to x(say). Step 2: Determine the number of digits after the decimal point which do not have bar on them. Let there be n digits without bar just after the decimal point. Step 3: Multiply both sides of x by $10^{n}$ so that only the repeating decimal is on the right side of the decimal point. Step 4: Use the method of converting pure recurring decimal to the form $frac{p}{q}$ and obtain the value of x. Illustration: Express $15.7overline{12}$ each of the following mixed recurring decimals in the form $large frac{p}{q}.$ Solution: Let x = $15.7overline{12}$ . Then, As there is only one digit after the decimal point which do not have bar so multiply both sides with 10 $10x=157.overline{12}$ 10x = 157.121212.... .......[1] As two digits are repeating multiply both sides with 100 $large Rightarrow$ 1000x = 15712.1212... .......[2] On subtracting (1) from (2) , we get 990x = 15555 $Rightarrow ;;;x=frac{15555}{990}=frac{3111}{198}=frac{1037}{66}$ $Rightarrow ;;;15.7overline{12}=frac{1037}{66}$
Number Line using Successive Magnification We know that on a number line between any two points infinite number of point exist. So any number can be plotted on the number line by magnifying the line between two points, Number Line using Successive Magnification: To visualize the position (or representation) of numbers in decimal form the steps are 1. Analyse the given number and find the two points between which the number will lie. 2. Magnify the line between these two points.and find points with one decimal point between which the number will lie. 3. Repeat the step 2 for each decimal point. This process of visualization of numbers on the number line, through a magnifying glass, is known as the process of successive magnification. Illustration: To visualize the representation of 5.28 on the number line. Solution:We observe that 5.28 lies between 5 and 6. So, let us look closely at the position of the number line between 5 and 6. 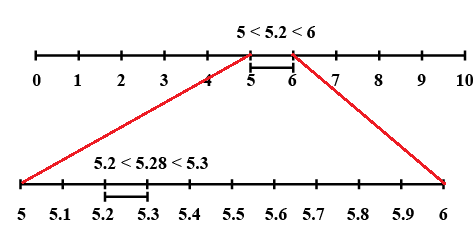We divide this portion into 10 equal parts and mark each point of division as shown in figure below This first mark to the right of 5 will represent 5.1, the second 5.2 and so on. To see this clearly, we magnify this portion by taking magnifying glass and look at the portion between 5 and 6. Through magnifying glass this portion between 5 and 6. As. 5.28 lies between 5.2 and 5.3. 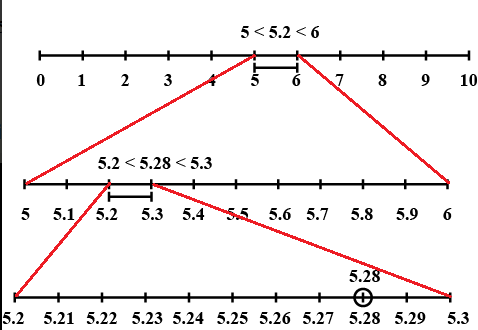So, let us mark 5.2 and 5.3 and magnify the portion between them We will again divide this portion into 10 equal parts and mark each point of division as shown in figure below This first mark to the right of 5.2 will represent 5.21, the second 5.22 and so on. To see this clearly, we magnify this portion by taking magnifying glass and look at the portion between 5.2 and 5.3 . The required point is 5.28 This process of visualization of numbers on the number line, through a magnifying glass, is known as the process of successive magnification.
Plotting any Irrational Numbers On a Number Line Plotting any Irrational Numebrs On a Number Line: For any positiv real number x, we have $large sqrt{left ( frac{x+1}{2}right )^{2}-left ( frac{x-1}{2} right )^{2}}=sqrt{frac{x^{2}+2x+1}{4}-frac{x^{2}-2x+1}{4}}=sqrt{frac{4x}{4}}=sqrt{x}$ Therefore, to find the positive square root of a positive real number, we may follow the following algorithm. ALGORITHM: STEP I Obtain the positive real number x(say) STEP II Draw a line and mark a point A on it. STEP III Mark a point B on the line such that AB = x units. STEP IV From point B mark a distance of 1 unit and mark the new poiint as C. STEP V Find the mid-point of AC and mark the point as O. STEP VI Draw a circle with centre O and radius OC> STEP VII Draw a line perpendicular to AC passing through B and intersecting the semi-circle at D. Length BD is equal to $large sqrt{x}.$ Justification: We have, AB = x units and BC = 1 unit. $large therefore$ AC = (x + 1) units $large Rightarrow ;;OA = OC = frac{x+1}{2};units$ $large Rightarrow ;; OD= frac{x+1}{2};units$ $large [because ;OA=OC=OD]$ Now, $large OB=AB-OA=x-frac{x+1}{2}=frac{x-1}{2}$ Using Pythagoras Theorem in $large Delta OBD,$ we have $OD^{2}=OB^{2}+BD^{2}$ $Rightarrow ;;BD^{2}=OD^{2}-OB^{2}$ $Rightarrow ;;BD^{2}=left ( frac{x+1}{2} right )^{2}-left ( frac{x-1}{2} right )^{2}$ $Rightarrow ;;BD=sqrt{frac{(x^{2}+2x+1)-(x^{2}-2x+1)}{4}}=sqrt{frac{4x}{4}}=sqrt{x}$ This shows that $sqrt{x}$ exists for all real numbers x > 0. In order to find the position of $sqrt{x}$ on the number line, we consider BC as the number line, with B as the origin to represent zero. Since BC = 1 so, C represents 1. Now, mark points $C_{1},C_{2},C_{3},......$ such that $CC_{1}=BC$ = 1, $C_{1}C_{2}=BC=1$ and so on. Clearly, $C_{1}C_{2},C_{3},.....$ represent 2, 3, 4,... respectively. Now, draw an arc with centre at B and radius equal to BD. Suppose this arc cuts the number line BC with B as the origin at E. Then, BE = $sqrt{x}$ . Consequently, E will represent $sqrt{x}$ .
Rationalization RATIONALIZATION: Let a and be positive real numbers.Then, $large (i)(sqrt{a}+sqrt{b})(sqrt{a}-sqrt{b})=a-b$ $large (ii)(a+sqrt{b})(a-sqrt{b})=a^{2}-b$ $large (iii)(sqrt{a}pm sqrt{b})^{2}=apm 2sqrt{ab}+b$ $large (iv)(sqrt{a}+sqrt{b})(sqrt{c}+sqrt{d})=sqrt{ac}+sqrt{ad}+sqrt{bc}+sqrt{bd}$ Rationalisation of Denominator: Sometimes we come across expressions containing square roots in their denominators. Addition, subtraction, multiplication and division of such expressions in convenient if their denominators are free from square roots.To make the denominators free from square roots, we multiply the numerator and denominator by an irrational number. Such a number is called rationalisation factor. Consider the expression $large frac{3+sqrt{5}}{sqrt{2}}$ . We know that $large sqrt{2}timessqrt{2}=2.$ Therefore, to remove the square root from the denominator we multiply its numerator and denominator by $large sqrt{2}$ . $large therefore$ $large frac{3+sqrt{5}}{sqrt{2}}=frac{3+sqrt{5}}{sqrt{2}timessqrt{2}}=sqrt{2}=frac{3sqrt{2}+sqrt{5}timessqrt{2}}{2}=frac{3sqrt{2}+sqrt{10}}{2}$ Let us now consider the expression $large frac{1}{2+sqrt{3}}$ We know that $large (a+sqrt{b})(a-sqrt{b})=a^{2}-b$ $large therefore$ $large (2+sqrt{3})(2-sqrt{3})=4-3=1,$ which is a rational number So, we multiply the numerator and denominator by $large 2-sqrt{3}$ $large therefore ;frac{1}{2+sqrt{3}}=frac{1}{2+sqrt{3}}timesfrac{2-sqrt{3}}{2-sqrt{3}}=frac{2-sqrt{3}}{4-3}=2-sqrt{3}$ Example: If $large x=2+sqrt{3},$ find the valur of $large x^{2}+frac{1}{x^{3}}$ SOLUTION We have, $large x=2+sqrt{3},$ $large therefore$ $large frac{1}{x}=frac{1}{2+sqrt{3}}=frac{1}{2+sqrt{3}}timesfrac{2-sqrt{3}}{2-sqrt{3}}=frac{2-sqrt{3}}{2^{2}-(sqrt{3})^{2}}=frac{2-sqrt{3}}{4-3}=2-sqrt{3}$ Now, $large x^{2}+frac{1}{x^{2}}=left ( x+frac{1}{x} right )^{2}-2$ $large Rightarrow ;;x^{2}+frac{1}{x^{2}}=(2+sqrt{3}+2-sqrt{3})^{2}-2=4^{2}-2=16-2=14$

Want Help?